A Happy World? What Makes a State and it's Citizens Happy?
Zakaria Imessaoudene - Statistics for International Relations Research II
- I. INTRODUCTION
- II. DATA & VISUALIZATION
- III. METHODOLOGY
- IV. REGRESSION MODELS
- V. RESULTS & DISCUSSION
- VI. REFERENCES
- VII. APPENDIX
I. INTRODUCTION
The COVID-19 pandemic has certainly forced societies around the world to adapt to a period defined by social distancing, hardship, lock-down, and confinement. Although this pandemic brought with it many challenges and uncertainty, it also provided many people an opportunity to step back and reflect. While taking this course virtually, I became interested in the question: what factors make a country and its citizens happy? Curious, I searched for data that could help me answer this question. Alas, I stumbled upon the United Nation’s Sustainable Development Solutions Networks’ (UNSDSN) annual World Happiness Report for 2019. According to the organization, the annual report incorporates a “survey of the state of global happiness that ranks 156 countries by how happy their citizens perceive themselves to be. The World Happiness Report 2019 focuses on happiness and the community: how happiness has evolved over the past dozen years, with a focus on the technologies, social norms, conflicts and government policies that have driven those changes” (Helliwell et al. 2019). Therefore, considering the ongoing global pandemic and the utterly abysmal social conditions it has wrought, we could also use some positivity and “happiness” right now. Why not look more into this?
“Happiness” is a very subjective experience thus, when assessing this emotion, surveys can help assess a certain average. Indeed, in trying to gauge this estimate, the UNSDSN relies on data derived from surveys for social wellbeing carried out by the Gallup World Poll to build their report. In order to calculate the average national happiness score, the Gallup World Poll asks participants (in their respective language) to answer the following question: “Please imagine a ladder, with steps numbered from 0 at the bottom to 10 at the top. The top of the ladder represents the best possible life for you and the bottom of the ladder represents the worst possible life for you. On which step of the ladder would you say you personally feel you stand at this time?” While this is a bit broad, it provides some outlook on general perceptions of wellbeing within a country.
Of course, there has been some debate around using the term “happiness” to define subjective estimates of one’s wellbeing. As Helliwell (2020: 180) highlights, happiness “plays two important roles within the science of wellbeing, appearing once as a prototypical positive emotion and again as part of a cognitive life evaluation question.” True, “happiness” is a broad term that can take into account a variety of factors, but it too affects some social and even economic factors, suggesting mutual relationships. Nevertheless, through this project, I hope to look at the major factors that the UNSDSN considers to be important while looking into whether population size plays a role in overall happiness. Since the UNSDSN’s annual World Happiness Report is one of the most respected reports used by states to guide public policy, I will use the same data provided by the organization to learn more about the relationships between happiness and several indicators.
After looking at the literature on life satisfaction and public policy (which tend to be in economics), it appears that economic growth (i.e., GDP per Capita) increases wellbeing. In Deaton’s (2008: 69) work, he indicates that there is a “very strong global relationship between per capita GDP and life satisfaction [which] suggests that on average people have a good idea of how income, or the lack of it, affects their lives.” Easterlin (2013) disputes this finding, citing evidence that higher economic growth rates are not accompanied by greater increments in happiness for a wide range of developed, developing, or transition countries (including China). Rather Easterlin (2013) suggests that social support (i.e., welfare) plays a significant role in happiness. Indeed, he notes that respondents living in “ultra-welfare states give consistently higher ratings for a wide range of public services: health, education, care of children and the elderly, and public pensions…express[ing] greater trust in the political system” (Easterlin 2013: 9). Where the two agree is on health where access to good health services or life expectancy, as an indicator of health, yield statistically significant results on happiness. As Deaton (2008: 69) underscores, “without health, there is very little that people can do, and without income, health alone does little to enable people to lead a good life.” Therefore it would be interesting to see how these variables are linked together via an interaction term later in this study.
Furthermore, when thinking about what would constitute a happy country, it would not be wrong to assume that good governance (i.e., political stability, distribution of state resources, and access to good services) would lie at the root of the question. Therefore, using the data provided by the UNSDSN, I will rely on OLS (multiple linear regression) models to track the relationship between the Happiness Score and independent variables such as Economy (GDP per capita), Social Support, Healthy (Life Expectancy), Generosity, and Trust (Government Corruption). Although the dataset already includes these variables, I am planning on adding other variables, such as a binary variable for the Population Size (large vs. small) and a categorical variable for the Region. I hope to see whether countries with smaller populations are happier than larger ones as well as which regions are happiest. In doing so, I aim to get a better idea of what makes countries happier while testing the two hypotheses below.
Ia. Hypotheses
Hypothesis 1: Countries with stronger economies (higher GDP per capita), longer life expectancy (i.e., better quality of life), greater freedom, and robust social services will be happier than those of the contrary.
Hypothesis 2: Countries with smaller populations will be happier than those with larger populations.
II. DATA & VISUALIZATION
In this section, I will introduce the happy2019_dta.csv I will be using for this short research project. This section will identify and discuss the response/dependent variable and the explanatory/independent variables, visualize the sample data and units of measurements, and discuss potential issues in the data such as missing data and questionable values.
IIa. Dataset
The happy.data_dta.csv dataset I will be using for this blog post is a combination of data used in the UNSDSN’s 2019 World Happiness Report alongside the World Bank’s population data. The 2019 World Happiness data contains 156 country observations which means that some states are missing. Regardless, when importing and merging the World Bank’s population data, I adhered to the 156 observations since the UNSDSN’s dataset contains most of the variables I am interested in using After merging the two datasets via Microsoft Excel, I added a categorical variable, “region,” to get a better understanding of the distribution of variables and happiness across ten (10) different regions. Indeed, while this project aims to get a better understanding of what factors affect happiness the most, it also seeks to answer why some regions are happier than others.
Identifying Variables
The dependent variable for this study will be “hscore” or the Happiness Score extrapolated from the 2019 World Happiness Report dataset - where the higher the score, the happier the country. The independent variables that will be used in this study are: GDP per capita (economy_gdpc), Life Expectancy (health), Social Support (govsupport), Freedom to make life choices (freedom), Generosity (generous), Trust (Government Corruption), and Population Size (small/large) (pop_size).
For Reference:
The categorical variable, region, was factored accordingly: North America (1), Latin America & Caribbean (2), Western Europe (3), Central & Eastern Europe (4), Middle East & North Africa (5), Sub-Saharan Africa (6) South Asia (7), East Asia (8), Southeast Asia (9), Australia & New Zealand (10).
The binary variable, pop_size, was broken down accordingly: Small (0), Large (1). The cutoff for a small or large population was derived from the median population size where populations less than or equal to 11.383 million were classified as small and those above this value were classified as large.
Importing, Cleaning, and Manipulating the Dataset
Please refer to the R-Markdown code to see how the data was imported, cleaned, and manipulated. You will find the following:
- R Package Library
- Renaming Variables
- Creating & Factoring Categorical and Binary Variables
IIb. Measurements, Descriptive Stats, and Distributions
10 Highest Ranked Countries - Happiness Score
10 Lowest Ranked Countries - Happiness Score
Taking a look at the ten highest and lowest ranking stats according to the happiness score reveals something interesting. The top 10 countries are located in Western Europe, North America, and Australia & New Zealand. Alternatively, the lowest ranking countries are located in Sub-Saharan Africa, South Asia, and the Middle East & North Africa. This preliminary observation could indicate that developed countries are happier than developing countries; however, more tests need to be done before making any conclusions.
Descriptive Statistics by Region
[1] "
| North America (N=2) | Latin America & Caribbean (N=21) | Western Europe (N=19) | Central & Eastern Europe (N=31) | Middle East & North Africa (N=19) | Sub-Saharan Africa (N=40) | South Asia (N=7) | East Asia (N=6) | Southeast Asia (N=9) | Australia & New Zealand (N=2) | Overall (N=156) | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| hscore | |||||||||||
| Mean (SD) | 7.09 (0.273) | 5.95 (0.724) | 6.94 (0.667) | 5.58 (0.571) | 5.24 (1.06) | 4.30 (0.625) | 4.53 (0.793) | 5.69 (0.476) | 5.27 (0.618) | 7.27 (0.0559) | 5.41 (1.11) |
| Median | 7.09 | 6.11 | 7.05 | 5.60 | 5.21 | 4.40 | 4.46 | 5.66 | 5.19 | 7.27 | 5.38 |
| region | |||||||||||
| North America | 2 (100%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 2 (1.3%) |
| Latin America & Caribbean | 0 (0%) | 21 (100%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 21 (13.5%) |
| Western Europe | 0 (0%) | 0 (0%) | 19 (100%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 19 (12.2%) |
| Central & Eastern Europe | 0 (0%) | 0 (0%) | 0 (0%) | 31 (100%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 31 (19.9%) |
| Middle East & North Africa | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 19 (100%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 19 (12.2%) |
| Sub-Saharan Africa | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 40 (100%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 40 (25.6%) |
| South Asia | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 7 (100%) | 0 (0%) | 0 (0%) | 0 (0%) | 7 (4.5%) |
| East Asia | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 6 (100%) | 0 (0%) | 0 (0%) | 6 (3.8%) |
| Southeast Asia | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 9 (100%) | 0 (0%) | 9 (5.8%) |
| Australia & New Zealand | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 2 (100%) | 2 (1.3%) |
| economy\_gdpc | |||||||||||
| Mean (SD) | 1.40 (0.0481) | 0.924 (0.210) | 1.37 (0.0988) | 1.04 (0.214) | 1.06 (0.347) | 0.455 (0.282) | 0.650 (0.211) | 1.24 (0.198) | 0.930 (0.309) | 1.34 (0.0488) | 0.911 (0.393) |
| Median | 1.40 | 0.960 | 1.37 | 1.07 | 1.04 | 0.380 | 0.677 | 1.31 | 0.807 | 1.34 | 0.960 |
| Missing | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 1 (2.5%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 1 (0.6%) |
| govsupport | |||||||||||
| Mean (SD) | 1.48 (0.0339) | 1.34 (0.173) | 1.50 (0.0967) | 1.33 (0.208) | 1.15 (0.263) | 0.940 (0.239) | 0.987 (0.297) | 1.33 (0.152) | 1.25 (0.141) | 1.55 (0.00636) | 1.22 (0.284) |
| Median | 1.48 | 1.40 | 1.50 | 1.39 | 1.23 | 0.939 | 0.928 | 1.35 | 1.20 | 1.55 | 1.27 |
| Missing | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 1 (2.5%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 1 (0.6%) |
| health | |||||||||||
| Mean (SD) | 0.957 (0.117) | 0.812 (0.106) | 1.01 (0.0232) | 0.825 (0.0905) | 0.751 (0.143) | 0.418 (0.138) | 0.617 (0.149) | 0.953 (0.168) | 0.745 (0.188) | 1.03 (0.00707) | 0.730 (0.236) |
| Median | 0.957 | 0.831 | 0.999 | 0.818 | 0.795 | 0.428 | 0.604 | 0.975 | 0.660 | 1.03 | 0.789 |
| Missing | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 1 (2.5%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 1 (0.6%) |
| freedom | |||||||||||
| Mean (SD) | 0.519 (0.0919) | 0.441 (0.128) | 0.487 (0.137) | 0.361 (0.114) | 0.318 (0.167) | 0.337 (0.118) | 0.451 (0.0743) | 0.372 (0.127) | 0.544 (0.0339) | 0.571 (0.0198) | 0.395 (0.140) |
| Median | 0.519 | 0.489 | 0.526 | 0.346 | 0.305 | 0.354 | 0.464 | 0.396 | 0.547 | 0.571 | 0.417 |
| Missing | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 1 (14.3%) | 0 (0%) | 0 (0%) | 0 (0%) | 1 (0.6%) |
| generous | |||||||||||
| Mean (SD) | 0.283 (0.00354) | 0.145 (0.0798) | 0.235 (0.0906) | 0.146 (0.0780) | 0.153 (0.0869) | 0.188 (0.0692) | 0.235 (0.0741) | 0.173 (0.0893) | 0.302 (0.149) | 0.331 (0.00141) | 0.186 (0.0944) |
| Median | 0.283 | 0.126 | 0.257 | 0.137 | 0.133 | 0.198 | 0.220 | 0.205 | 0.266 | 0.331 | 0.178 |
| Missing | 0 (0%) | 0 (0%) | 1 (5.3%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 1 (0.6%) |
| trust | |||||||||||
| Mean (SD) | 0.218 (0.127) | 0.0720 (0.0337) | 0.231 (0.127) | 0.0665 (0.0642) | 0.105 (0.0403) | 0.0945 (0.0690) | 0.0934 (0.0497) | 0.120 (0.0895) | 0.123 (0.136) | 0.335 (0.0636) | 0.111 (0.0944) |
| Median | 0.218 | 0.0740 | 0.265 | 0.0400 | 0.106 | 0.0855 | 0.0890 | 0.0985 | 0.0730 | 0.335 | 0.0860 |
| Missing | 0 (0%) | 0 (0%) | 0 (0%) | 1 (3.2%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 0 (0%) | 1 (0.6%) |
| pop\_in\_millions | |||||||||||
| Mean (SD) | 183 (206) | 29.9 (50.0) | 22.4 (27.1) | 13.3 (26.7) | 28.1 (30.3) | 25.6 (37.1) | 262 (494) | 268 (555) | 73.4 (82.9) | 15.2 (14.4) | 48.2 (161) |
| Median | 183 | 11.3 | 10.3 | 5.45 | 11.7 | 15.0 | 38.0 | 37.7 | 54.0 | 15.2 | 11.4 |
| pop\_size | |||||||||||
| Small | 0 (0%) | 11 (52.4%) | 12 (63.2%) | 25 (80.6%) | 9 (47.4%) | 15 (37.5%) | 1 (14.3%) | 2 (33.3%) | 2 (22.2%) | 1 (50.0%) | 78 (50.0%) |
| Large | 2 (100%) | 10 (47.6%) | 7 (36.8%) | 6 (19.4%) | 10 (52.6%) | 25 (62.5%) | 6 (85.7%) | 4 (66.7%) | 7 (77.8%) | 1 (50.0%) | 78 (50.0%) |
"
IIc. Missing Data & Diagnostics
In this subsection, I analyze the data by conducting a series of tests to check the robustness of the dataset and make sure there are no causes for alarm before creating models. For instance, I start by checking whether or not there are missing data values, followed by observing the overall distribution of the dependent value as well as by region. Afterward, I look for any correlations between variables as well as outliers. Finally, after these checks are done, I create preliminary OLS models that will serve further tests to discover the absence or presence of heteroskedasticity.
Because missing values in data are a common problem, I use the Amelia package (first tab) and the Mice package (second tab) to get a better view of my dataset. Looking at the graphs, it appears that there are six (6) missing values for different observations. In other words, the observations with missing data have no more than one missing value. Regardless of these gaps, the percentage of missing data is so low that the function returns a score of 0%. Therefore, the statistical power of the regression models that will be created below will not be significantly reduced.
If a dataset still maintains a large number of observations, then one way to deal with missing data is to delete or omit missing values from the observations or rows that contain these gaps. Furthermore, this results in complete data. Although this makes the data cleaner to use, can reduce the sample size and statistical power. However, as mentioned above, the missing data are so few that it will not affect the statistical power of our models.
Missingness Map
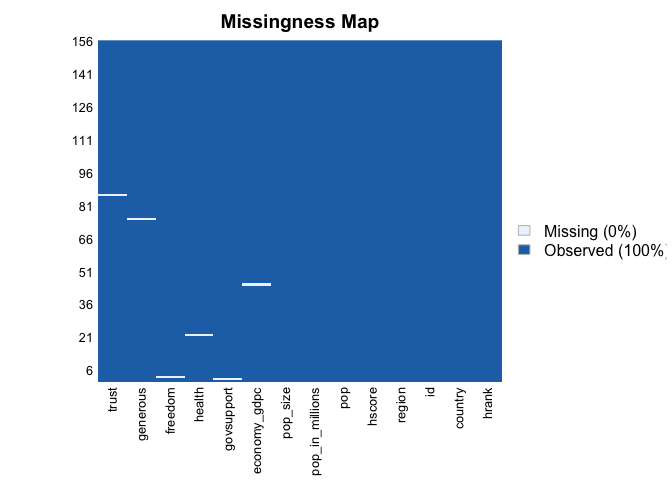
Missing Data Pattern
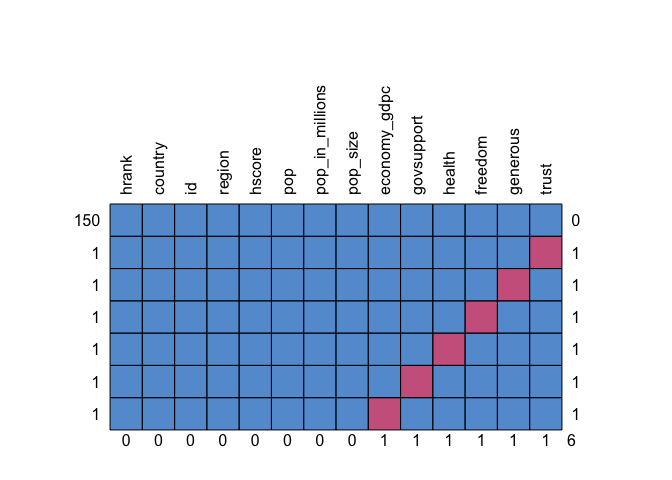
Omitting Data
Therefore, I will update the dataset by omitting the missing values.
happy.data <- na.omit(happy.data)
view(happy.data)
IId. Distribution of Variables
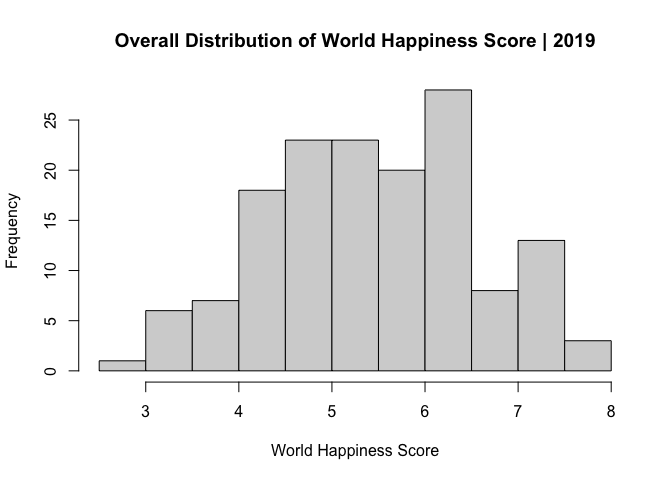
When viewing the distribution of the dependent variable (hscore), it appears that the distribution is slightly skewed to the right; however, it is still relatively normal.
Distribution of Variables (mean score) by Region
Mean Value Distribution of Happiness Score by Region
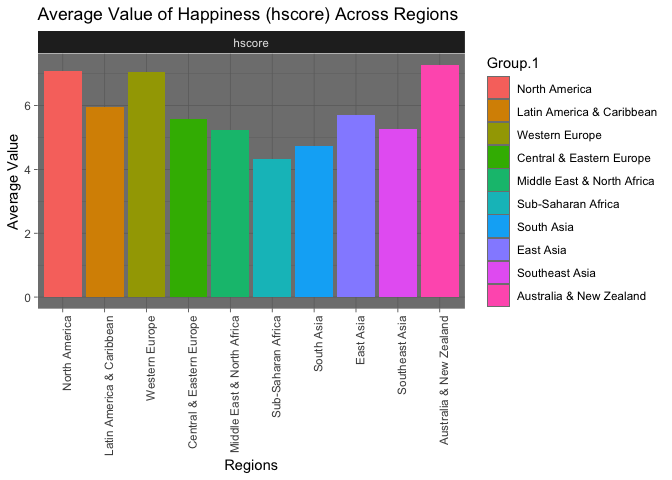
After calculating the mean scores for each variable for each region, it appears that North America, Western Europe, and Australia & New Zealand were the happiest regions in the world in 2019. Contrarily, the Middle East & North Africa, Sub-Saharan Africa, and South Asia were the least happy regions in the world in 2019. Economic disparities among the regions as well as varying levels of political freedoms could have played an integral role in this outcome.
Mean Value Distribution of GDP per capita, Social Support, and Life Expectancy by Region
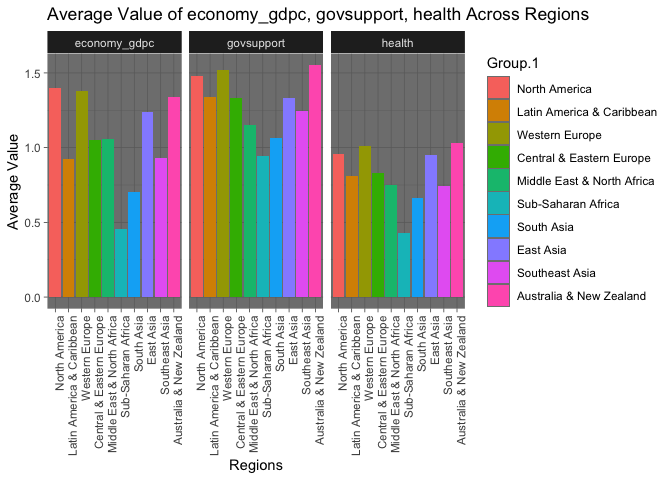
Continuing along this analysis, it appears that there is repeating pattern. The three happiest regions outlined above are also the top performers among these three variables. The opposite is also true.
Mean Value Distribution of Freedom, Generosity, and Trust (Government Corruption) by Region
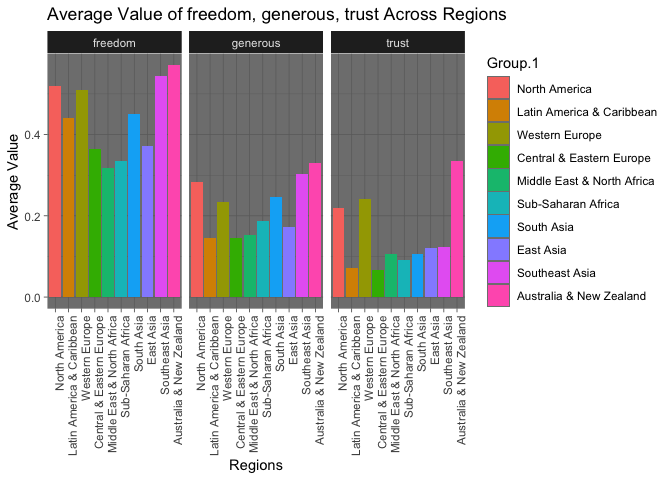
The distribution of values for this series of variables is quite interesting. In terms of freedom, the top performers are Australia & New Zealand, Southeast Asia, and North America (Western Europe comes in fourth); however, the lowest performers are Central Europe, the Middle East & North Africa, and Sub-Saharan Africa. Generosity and Trust in one’s government show similar trends in terms of top performers but changes among the lowest performers.
Distribution of Happiness Score via Boxplot
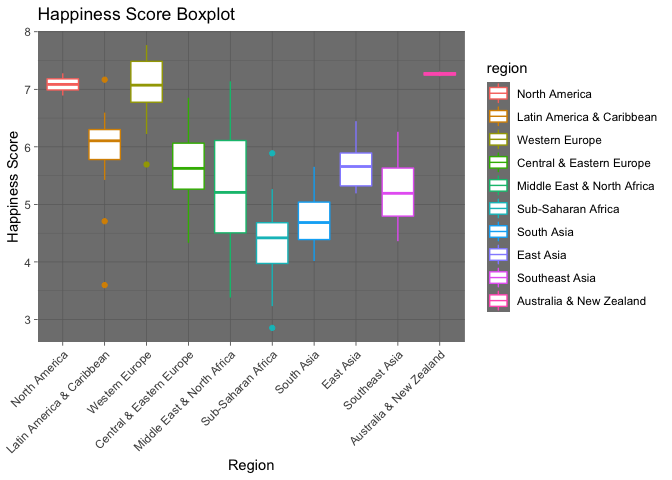
The boxplot above shows the distribution of happiness scores (the dependent variable), by region. Again, it is clear that North America, Western Europe, and Australia & New Zealand have the highest hscores relative to other regions. Another point worth noting is the Middle East & North Africa region has the largest range of scores comparatively.
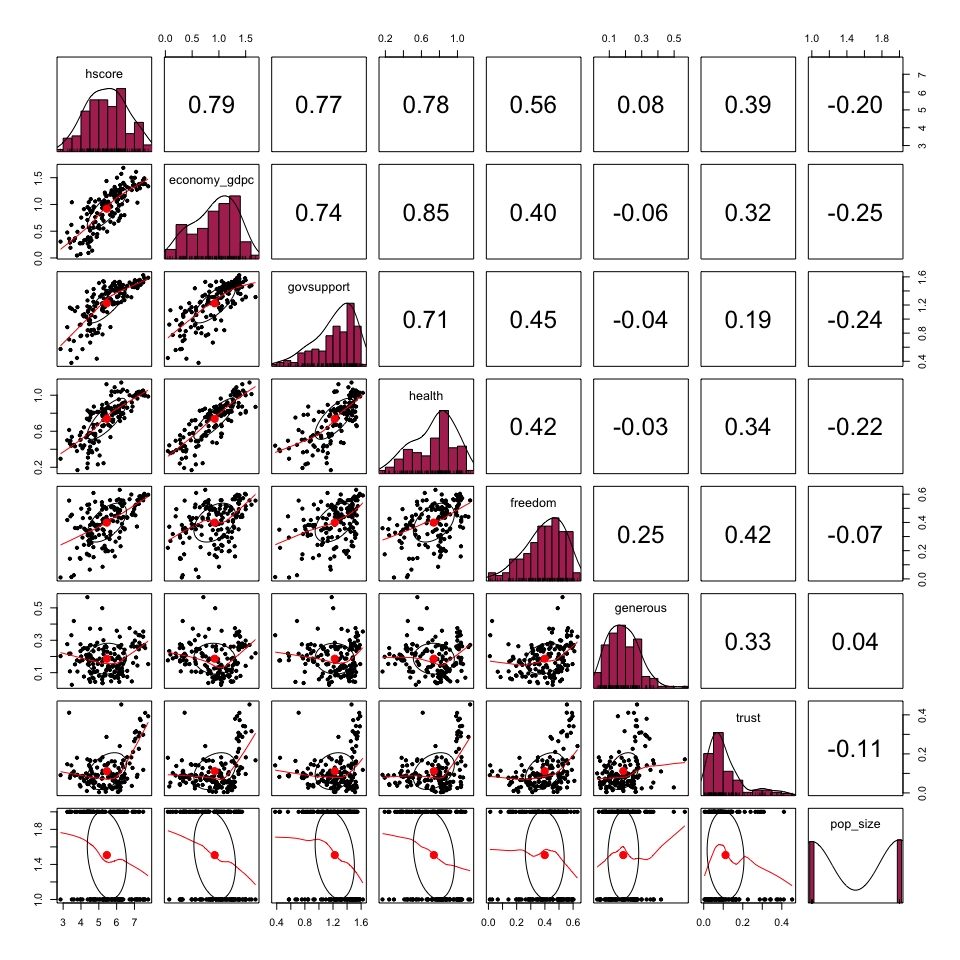
IIe. Correlation Analysis
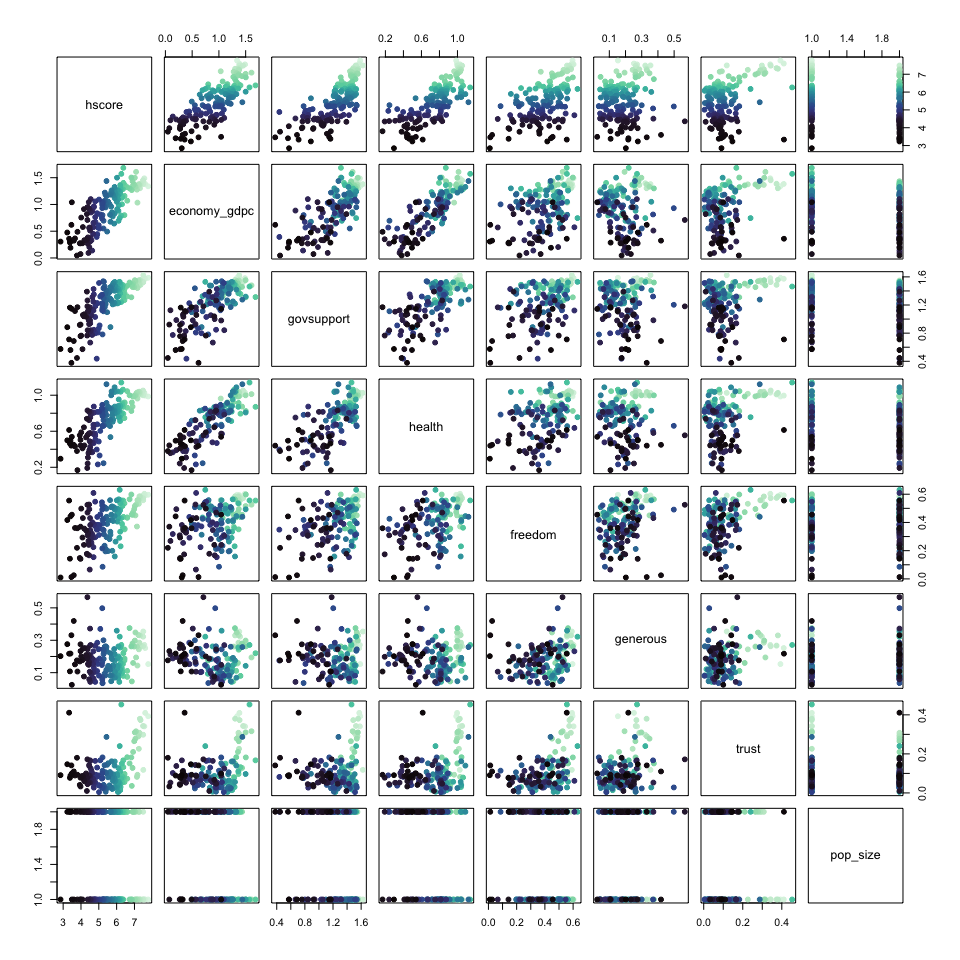
Relying on a correlation matrix, can give us a better understanding of the relationship between the dependent variable (hscore) and relevant independent variables. As the matrix above shows, hscore has a strong positive linear relationship with economy_gdpc, govsupport, and health. Additionally, it appears that the generous and trust variables have little to no relationship with hscore, whereas, the relationship between freedom and hscore is positive but quite weak.
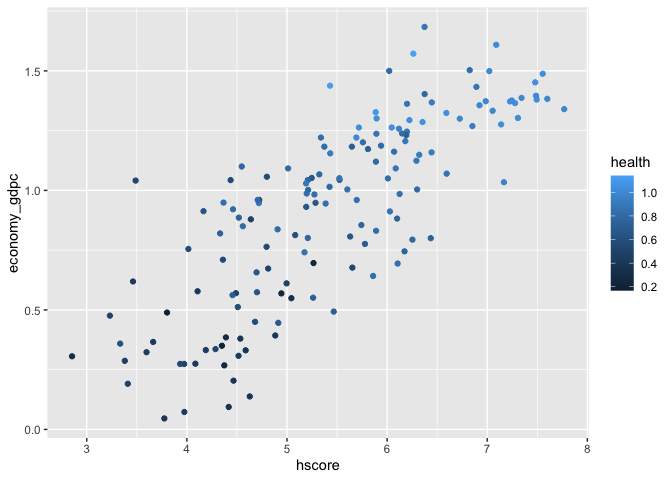
Relationship Between Happiness Score, Health (Life Expectancy), and Economy (GDP per capita)
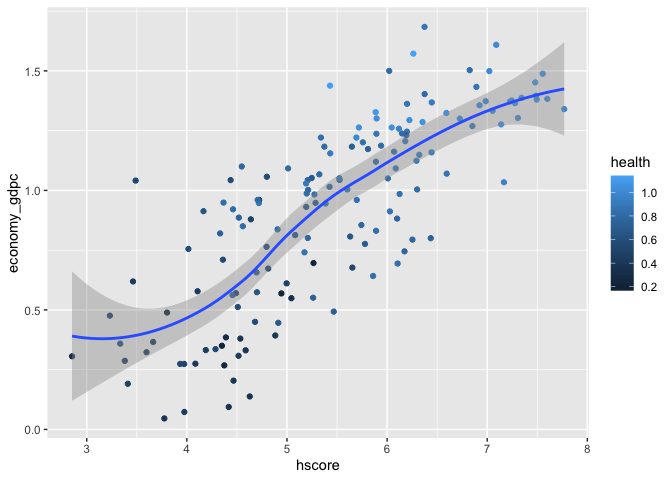
It appears that the happiness score, health (life expectancy), and economy (GDP per capita) share a positive linear relationship. For instance, as the graph below shows, the higher the health and economy value, the higher the happiness score. Moreover, as indicated by the color gauge for health score, it appears that health (life expectancy) plays a significant effect on the happiness score. Although the line of best fit (tab 2) returns a slightly sigmoidal relationship, the relationship between these variables is more or less linear.
Scatter Plot
Scatter Plot with Fitted Line
III. METHODOLOGY
For this project, I will use an extension of ordinary least-squares regression (OLS), specifically, multiple linear regression models, to test my hypotheses. Multiple linear regression models are the logical choice for this study since (1) I have one dependent variable (hscore) and multiple independent variables, and (2) I am curious to see the (non)linear relationship between my response/dependent variable and explanatory/independent variables. Since happiness is a subjective emotional experience, it is predicated on a compendium of factors. Therefore, at the macro level (i.e., country-level), I hope to get a better sense of what main factors affect happiness, in general, across the world.
In using multiple linear regression models, there are certain assumptions the must be taken into consideration:
- There is a linear relationship between the dependent variable and independent variables.
- The residuals, the difference between the observed value of the dependent variable and its predicted value, are normally distributed around a mean of 0.
- The independent variables are not highly correlated with each other. In other words, there is no major sign of multicollinearity.
IV. REGRESSION MODELS
IVa. Modelling - Multiple Linear Regressions (MLR)
| Model 1 | Model 2 | Model 3 | Model 4 | Model 5 | Model 6 | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Predictors | Estimates | std. Error | CI | Estimates | std. Error | CI | Estimates | std. Error | CI | Estimates | std. Error | CI | Estimates | std. Error | CI | Estimates | std. Error | CI |
| (Intercept) | 1.66 \*\*\* | 0.24 | 1.19 – 2.12 | 1.68 \*\*\* | 0.23 | 1.22 – 2.14 | 1.66 \*\*\* | 0.25 | 1.16 – 2.15 | 2.77 \*\*\* | 0.40 | 1.97 – 3.56 | 3.97 \*\*\* | 0.68 | 2.63 – 5.31 | 2.90 \*\*\* | 0.60 | 1.72 – 4.09 |
| economy\_gdpc | 0.86 \*\*\* | 0.23 | 0.41 – 1.32 | 0.80 \*\*\* | 0.23 | 0.34 – 1.26 | 0.81 \*\*\* | 0.23 | 0.35 – 1.27 | -0.72 | 0.49 | -1.69 – 0.26 | -0.56 | 0.54 | -1.63 – 0.50 | 0.95 \*\*\* | 0.23 | 0.48 – 1.41 |
| govsupport | 1.14 \*\*\* | 0.25 | 0.65 – 1.64 | 1.22 \*\*\* | 0.25 | 0.72 – 1.73 | 1.23 \*\*\* | 0.26 | 0.73 – 1.74 | 1.24 \*\*\* | 0.25 | 0.75 – 1.73 | 0.89 \*\*\* | 0.24 | 0.42 – 1.37 | 0.84 \*\*\* | 0.25 | 0.35 – 1.33 |
| health | 1.12 \*\* | 0.38 | 0.38 – 1.87 | 1.05 \*\* | 0.38 | 0.30 – 1.79 | 1.05 \*\* | 0.38 | 0.30 – 1.80 | -0.71 | 0.63 | -1.95 – 0.53 | -1.40 | 0.76 | -2.90 – 0.09 | 0.53 | 0.44 | -0.33 – 1.40 |
| freedom | 1.59 \*\*\* | 0.38 | 0.84 – 2.35 | 1.41 \*\*\* | 0.39 | 0.63 – 2.19 | 1.40 \*\*\* | 0.40 | 0.62 – 2.18 | 1.65 \*\*\* | 0.39 | 0.89 – 2.42 | 1.83 \*\*\* | 0.40 | 1.04 – 2.61 | 1.61 \*\*\* | 0.40 | 0.82 – 2.41 |
| generous | 0.73 | 0.49 | -0.23 – 1.70 | 0.48 | 0.51 | -0.52 – 1.48 | 0.48 | 0.51 | -0.53 – 1.48 | 0.23 | 0.50 | -0.75 – 1.21 | 0.54 | 0.51 | -0.46 – 1.54 | 0.76 | 0.52 | -0.27 – 1.78 |
| trust | 0.95 | 0.56 | -0.15 – 2.06 | 0.97 | 0.56 | -0.14 – 2.08 | 0.01 | 0.61 | -1.20 – 1.21 | -0.44 | 0.61 | -1.64 – 0.76 | 0.05 | 0.60 | -1.14 – 1.25 | |||
| pop\_size | 0.03 | 0.09 | -0.15 – 0.21 | 0.02 | 0.09 | -0.15 – 0.20 | 0.05 | 0.09 | -0.12 – 0.23 | 0.04 | 0.09 | -0.14 – 0.22 | ||||||
| economy\_gdpc \* health | 2.16 \*\*\* | 0.63 | 0.92 – 3.40 | 2.14 \*\* | 0.69 | 0.77 – 3.52 | ||||||||||||
| region | -0.07 | 0.39 | -0.84 – 0.70 | -0.23 | 0.40 | -1.01 – 0.56 | ||||||||||||
| region | -0.06 | 0.36 | -0.77 – 0.65 | -0.02 | 0.37 | -0.75 – 0.72 | ||||||||||||
| region | -0.43 | 0.38 | -1.19 – 0.32 | -0.58 | 0.39 | -1.36 – 0.19 | ||||||||||||
| region | -0.53 | 0.38 | -1.29 – 0.23 | -0.69 | 0.39 | -1.47 – 0.09 | ||||||||||||
| region | -0.78 | 0.41 | -1.60 – 0.04 | -0.74 | 0.43 | -1.59 – 0.10 | ||||||||||||
| region | -0.81 | 0.42 | -1.65 – 0.03 | -1.02 \* | 0.43 | -1.87 – -0.17 | ||||||||||||
| region | -0.77 | 0.40 | -1.56 – 0.02 | -0.78 | 0.41 | -1.59 – 0.04 | ||||||||||||
| region | -0.96 \* | 0.39 | -1.74 – -0.19 | -1.10 \*\* | 0.40 | -1.89 – -0.30 | ||||||||||||
| region | 0.05 | 0.48 | -0.90 – 1.00 | 0.03 | 0.50 | -0.95 – 1.02 | ||||||||||||
| Observations | 150 | 150 | 150 | 150 | 150 | 150 | ||||||||||||
| R2 / R2 adjusted | 0.766 / 0.758 | 0.770 / 0.761 | 0.771 / 0.759 | 0.789 / 0.777 | 0.834 / 0.813 | 0.822 / 0.801 | ||||||||||||
| AIC | 248.885 | 247.851 | 249.763 | 239.588 | 221.040 | 229.500 | ||||||||||||
| ||||||||||||||||||
IVb. Model Selection
When it comes to model selection, it is important to select the model that is the most parsimonious and fits the data well. In order to do so, we can rely on two estimates to help us make a decision, the Adjusted R2 and the Akaike Information Criterion (AIC). The Adjusted R2 indicates how well data points fit on a regression line while adjusting for the number of terms in a model, whereas, the AIC compares models and determine which one best fits the data. In this case, Model 5 is the best model to use since it has the highest Adjusted R2 value (0.813), and lowest AIC score (221.040). Another way to make sure which model to pick is by carrying an ANOVA test.
After comparing the three highest-scoring models (Model 4, Model 5, and Model 6) via an ANOVA test, it appears that testing additional variables increases the statistical significance. As indicated by the F-Statistic, Model 5 has the highest statistical significance; indicating that Model 5 is the best model to use. It is worth mentioning that Model 4 comes in as a close second.
NOTE: Model 3 was used as the reference/baseline group.
IVc. Model Diagnostics & Assumptions Test
Multicollinearity
After selecting the regression model, the next step is to test for multicollinearity via the variance inflation factor (or VIF). The R function vif() from the car package can help us detect the presence of multicollinearity in our regression model (Model 5) by measuring how much the variance of a regression coefficient is inflated due to multicollinearity in the model. As a rule of thumb, VIF values that exceed 5 or 10 indicate a problematic amount of collinearity (James et al. 2014). Therefore, after calling the vif() function on Model 5, it appears that multicollinearity is present with “region” (GVIF = 22.531739). This suggests that we update the model by removing this predictor variable. Fortunately, Model 4 addresses this issue since it tests the same independent variables bar “region.”
While it is true that the “economy_gdpc” and “health” variables are also above a threshold of 5 or 10, the high VIF values for these predictor variables are a result of the interaction term that is present in the model. Additionally, as the ANOVA test above shows, the coefficients in Model 4 are still statistically significant at the 99% level (refer to F-statistic). Thus, I will use Model 4 since it solves the issue of multicollinearity and does not compromise model accuracy, ergo, a good model.
vif(lm5)
## GVIF Df GVIF^(1/(2*Df))
## economy_gdpc 29.046748 1 5.389504
## health 19.691880 1 4.437553
## govsupport 2.998553 1 1.731633
## freedom 1.968333 1 1.402973
## generous 1.534215 1 1.238635
## trust 2.170744 1 1.473344
## pop_size 1.288556 1 1.135146
## region 22.531739 9 1.188927
## economy_gdpc:health 65.914803 1 8.118793
vif(lm4)
economy_gdpc health govsupport freedom
20.453171 11.309055 2.631177 1.588490
generous trust pop_size economy_gdpc:health
1.236928 1.825298 1.081174 44.887179
Linearity, Normality, Homoskedasticity, and Outliers
Linearity
After testing for non-linearity, it appears that relationships between variables in Model 4 are liner. This can be seen in both plots. For plot 2 (bottom), linear regression fits are shown for both y by x and x by y as well as correlation ellipses.
Normality
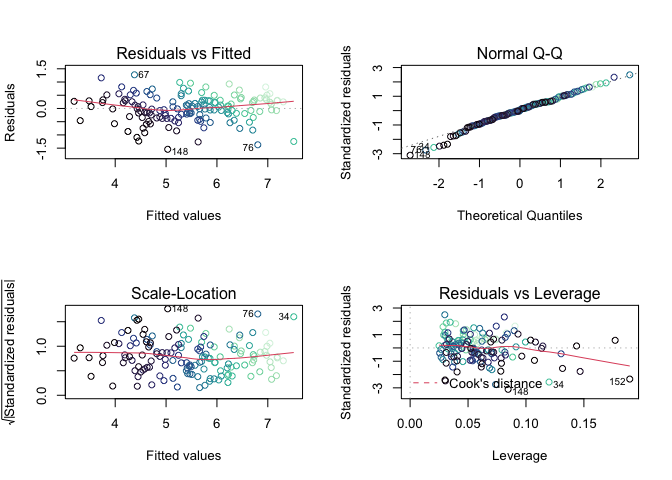
Looking at the Normal Q-Q plot, it appears that the residuals are normally distributed as most points lie on the line. While both ends reveal some variance, as indicated by the deviations (outliers) from the regression lines, the slight variance lies at the ends of the line (below -2 and above 2). Moreover, looking at the Residual vs. Fitted plot indicates that the residual points are normally distributed as the points are evenly distributed around the middle values. This is further reinforced by the Scale-Location plot as the
Another way to interpret the residual plot is to test for the distribution of the residuals via a series of normality tests - namely the Shapiro-Wilk (considered to be the most robust/significant). Normality tests are used to determine if a dataset is well-modeled by a normal distribution and compute how likely it is for a random variable underlying the data set to be normally distributed. Looking at the table below, both the Shapiro-Wilk (p = 0.1336) and Kolmogorov-Smirnov (p = 0.6705) tests have p-values greater than the 0.05 (95% level). Therefore, we can fail to reject the null hypothesis that the residuals are normally distributed.
## -----------------------------------------------
## Test Statistic pvalue
## -----------------------------------------------
## Shapiro-Wilk 0.986 0.1336
## Kolmogorov-Smirnov 0.0591 0.6705
## Cramer-von Mises 17.4628 0.0000
## Anderson-Darling 0.5686 0.1383
## -----------------------------------------------
Homoskedasticity.
studentized Breusch-Pagan test
data: lm4 BP = 14.535, df = 8, p-value = 0.06885
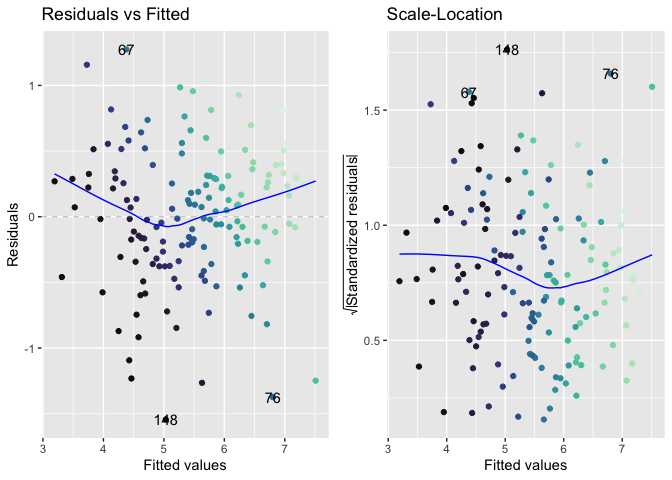
Going off of the Residual vs. Fitted model, there does not appear to any glaring sign of the infamous cone shape. Moreover, the residuals appear to be randomly distributed around the middle values. However, the Standardized Residuals vs. Fitted model tells a different story. Because the regression line is nearly linear, the model suggests homoskedasticity..
In order to be sure, I conducted a Breush-Pagan test. With a returned p-value of “0.06885”, greater than the p-value of 0.05, we can fail to reject the null hypothesis in favor of homoskedasticity.
Outliers
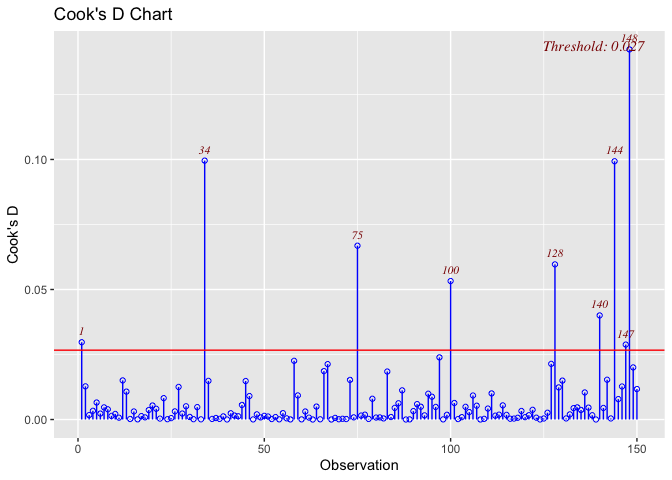
The Cook’s D values for observations 34, 75, 100, 128, 140, 144, and 148 each exceed the threshold of 0.027. Therefore, the plot above would suggest either further investigation or the removal of certain observations such as the 34th, 144th, and 148th observations. Indeed, by removing or resolving the issue with the most influential observation (as well as those already mentioned), the plot reveals that the model can be improved. However, while deleting these outliers is an option, it would not necessarily be the best plan of action, especially since they are real observations after all. There is a possibility that these outliers may indicate other trends or phenomena. Further investigation and research would need to be conducted before making this decision.
For reference, the outliers highlighted above are:
34 - Singapore (South East Asia)
75 - Croatia (Central & Eastern Europe)
100 - Nepal (South Asia)
128 - Mali (Sub-Saharan Africa)
140 - India (South Asia)
144 - Lesotho (Sub-Saharan Africa)
148 - Botswana (Sub-Saharan Africa)
NOTE: I ignored observations 1 and 147 since they are slightly about the threshold.
V. RESULTS & DISCUSSION
| Model 4 | Model 5 | |||||
|---|---|---|---|---|---|---|
| Predictors | Estimates | std. Error | CI | Estimates | std. Error | CI |
| (Intercept) | 2.77 \*\*\* | 0.40 | 1.97 – 3.56 | 3.97 \*\*\* | 0.68 | 2.63 – 5.31 |
| economy\_gdpc | -0.72 | 0.49 | -1.69 – 0.26 | -0.56 | 0.54 | -1.63 – 0.50 |
| health | -0.71 | 0.63 | -1.95 – 0.53 | -1.40 | 0.76 | -2.90 – 0.09 |
| govsupport | 1.24 \*\*\* | 0.25 | 0.75 – 1.73 | 0.89 \*\*\* | 0.24 | 0.42 – 1.37 |
| freedom | 1.65 \*\*\* | 0.39 | 0.89 – 2.42 | 1.83 \*\*\* | 0.40 | 1.04 – 2.61 |
| generous | 0.23 | 0.50 | -0.75 – 1.21 | 0.54 | 0.51 | -0.46 – 1.54 |
| trust | 0.01 | 0.61 | -1.20 – 1.21 | -0.44 | 0.61 | -1.64 – 0.76 |
| pop\_size | 0.02 | 0.09 | -0.15 – 0.20 | 0.05 | 0.09 | -0.12 – 0.23 |
| economy\_gdpc \* health | 2.16 \*\*\* | 0.63 | 0.92 – 3.40 | 2.14 \*\* | 0.69 | 0.77 – 3.52 |
| region | -0.07 | 0.39 | -0.84 – 0.70 | |||
| region | -0.06 | 0.36 | -0.77 – 0.65 | |||
| region | -0.43 | 0.38 | -1.19 – 0.32 | |||
| region | -0.53 | 0.38 | -1.29 – 0.23 | |||
| region | -0.78 | 0.41 | -1.60 – 0.04 | |||
| region | -0.81 | 0.42 | -1.65 – 0.03 | |||
| region | -0.77 | 0.40 | -1.56 – 0.02 | |||
| region | -0.96 \* | 0.39 | -1.74 – -0.19 | |||
| region | 0.05 | 0.48 | -0.90 – 1.00 | |||
| Observations | 150 | 150 | ||||
| R2 / R2 adjusted | 0.789 / 0.777 | 0.834 / 0.813 | ||||
| AIC | 239.588 | 221.040 | ||||
| ||||||
After creating the multiple linear regression models above and after carrying out the series robustness tests, it appears that we can answer the two hypotheses laid out in the introduction using Model 4.
Hypotheses
Hypothesis 1:
- Looking at Model 4, it appears that Social Support, Freedom to Make Life Choices, and the interaction term between GDP per capita & Life Expectancy are all (extremely) statistically significant at the 99.99% level (p<0.001). This finding supports the first hypothesis that countries with stronger economies (higher GDP per capita), longer life expectancies (better quality of life), greater freedom, and robust systems of government support will be happier than those of the contrary. After splitting the 156 (later 150) countries into different regions, it makes sense why North America, Australia & New Zealand, and Western Europe were among the top scorers. Countries in these regions are wealthy and have robust systems of governance. Referring back to the literature, Easterlin’s (2013) argument that employment and strong welfare policies increase happiness appears to be true as the variables with the most significant coefficients reflect state policies. Consequently, the top performers in terms of happiness (e.g., Finland, Denmark and Norway) - as seen in the Section IIb - are considered to have robust welfare systems.
Hypothesis 2:
- When it comes to hypothesis 2, it appears that population size, split between large and small, does not play a significant effect on a country’s happiness score. It was assumed that the larger the country (in terms of population), the harder it would be to provide social services, effectively redistribute resources, and add a level of competition among citizens. It turns out that this is not true. I will note that when testing population size on happiness score in a bivariate model, the results indicate that population size leads to a statistically significant (p<00.5) negative relationship with the happiness score. However, given that it is a bivariate model, no other variables were used as control, thus making the model weak.
Other Findings
- Although Model 5 did not pass the VIF test, the test detected multicollinearity in the regression analysis with regards to the “region” variable. Although this study is concerned with the relationship between happiness (or the happiness score of a country) with several explanatory variables to paint a better picture as to what affects happiness, Model 5 still holds relevant theoretical findings. Indeed, when comparing the regions with each other and controlling for the other variables, using North America as the reference category, it appears that each region is unhappy relative to North America, bar Australia & New Zealand. Additionally, Southeast Asia’s unhappiness appears to be statistically significant at the 95% level (p<0.05). Outside of this observation, the results are not statistically significant.
Va. Limitations
During my initial analysis of the 2019 World Happiness Report data, it appeared that there were no outliers or empty variables (i.e., NA). The one thing I should note is that instead of using NA (not applicable), the authors use 0.000 to indicate missing data. For instance, this can be seen in the social support in the Central African Republic. Although it is possible respondents did not believe social support exists in their country, it is highly unlikely that the value would be 0.000. Consequently, I cleaned the data by removing these values and leaving them blank. Furthermore, by removing this 0-value, I lost six observations after conducting the missingness tests above. Although this did not affect the statistical power of my models, as indicated by the missing data diagnostics, it is a limitation to this study.
Multiple Linear Regression, although provides useful insight into the relationship between certain variables, has its drawbacks. Because this study focuses on one year (2019), it is limited in its causal claims. This is especially the case when compared to longitudinal studies. Another limitation that I must address is that the number of variables used in the study was not exhaustive. True, they do a good job at highlighting major factors that affect happiness within a country; however, some nuances have to be addressed. For example, longer life expectancies do not necessarily indicate that everyone is happy since other factors could be at play. Quality of life estimates, on the other hand, could act as a valuable indicator for happiness; however, this is a broad category that is also composed of sub-factors such as purchasing power, political representation, feelings toward one’s local community, etc. Another point I would like to make is that the dataset did not account for whether a country is experiencing war or conflict, experiencing war, nor political transition periods (e.g., post-conflict). Indeed, there are so many factors that could affect happiness and vice-versa; therefore, there is plenty of room for more research.
Vb. Avenues for Future Research
- While the research provides some insight as to what factors make countries happy (in 2019), it by no means is exhaustive. More qualitative and quantitative research should be done to find new variables that could be linked to happiness. Using the same example from the last section, although life expectancy is typically used to assess overall health in a country, the general quality of life in a country could play a significant role in the perception of happiness. Of course, this variable (e.g., quality of life) will take into consideration multiple factors.
- Another suggestion is using panel data or cross-sectional time-series data to observation deviations in happiness among countries and regions throughout time. For example, given the recent (and ongoing) COVID-19 pandemic, it could be interesting to observe fluctuations in happiness.
- Lastly, there may be a correlation between good governance and happiness. Indeed, a crucial part of governing lies in providing quality public services to one’s constituents/citizens as well as distributing resources equitably and solving social issues promptly. Nevertheless, the relationship between the governed and the government could provide insight into general perceptions of happiness in “x” country. After looking at Model 4, one can assume that there is a relatively strong divide between developed and developing countries.
VI. REFERENCES
- Deaton, A. (2008). “Income, Health, and Well-being Around the World: Evidence from the Gallup World Poll”. Journal of Economic Perspectives, 22 (2), pp.53-72.
- Easterlin, R.A. (2013). “Happiness, Growth, and Public Policy”. Economic Inquiry, 51 (1), pp.1-15.
- Helliwell, J.F. (2020). “Three Questions About Happiness”. Behavioural Public Policy, 4 (2), pp.177-187.
- Helliwell, J., Layard, R., & Sachs, J. (2019). World Happiness Report 2019, New York: Sustainable Development Solutions Network.
- James, Gareth, Daniela Witten, Trevor Hastie, and Robert Tibshirani. (2014). An Introduction to Statistical Learning: With Applications in R. Springer Publishing Company, Incorporated.
VII. APPENDIX
Total Population & Happiness
| Model 7 - Happiness Score & Population | |||
|---|---|---|---|
| Predictors | Estimates | std. Error | CI |
| (Intercept) | 1.73 \*\*\* | 0.24 | 1.26 – 2.20 |
| economy\_gdpc | 0.82 \*\*\* | 0.23 | 0.37 – 1.28 |
| govsupport | 1.15 \*\*\* | 0.26 | 0.64 – 1.67 |
| health | 1.06 \*\* | 0.38 | 0.31 – 1.80 |
| freedom | 1.51 \*\*\* | 0.40 | 0.72 – 2.30 |
| generous | 0.45 | 0.51 | -0.55 – 1.45 |
| trust | 0.87 | 0.56 | -0.23 – 1.98 |
| pop\_in\_millions | -0.00 | 0.00 | -0.00 – 0.00 |
| Observations | 150 | ||
| R2 / R2 adjusted | 0.773 / 0.762 | ||
| AIC | 248.109 | ||
| |||
NOTE:: In the model above, while controlling for other independent variables, I tested the role of the total population on the happiness score to see if there was any effect. It turns out that the population of a country does not have a direct effect on happiness.
Bivariate Model: Population Size & Happiness
| Model 8 - Bivariate Population Size & Happiness | |||
|---|---|---|---|
| Predictors | Estimates | std. Error | CI |
| (Intercept) | 5.67 \*\*\* | 0.13 | 5.43 – 5.92 |
| pop\_size | -0.44 \* | 0.18 | -0.79 – -0.09 |
| Observations | 150 | ||
| R2 / R2 adjusted | 0.041 / 0.034 | ||
| AIC | 452.356 | ||
| |||
NOTE: In the bivariate model above, I attempted to see what the effect of population size was on the happiness score. It turns out that when a country reaches a certain population threshold (11.383), there will be a statistically significant negative relationship with happiness at the 95& level. Ergo, countries with large populations would have unhappy populations. However, because this is a bivariate model - does not consider any other independent variables - the explanatory power is very weak. This can be seen in the low R and Adjusted R2 values as well as the high AIC value.