Logistic Regression Report
Shanling Liu - Statistics for International Relations Research II
- 1. Introduction
- 2. Data and Visualization
- 3. Methods
- 4. Results
- 4.1 Model results and Diagnostics
- 4.2 Model Selection
- 4.3 The Interpretation of the Best Model
- 5. Conclusion
- References:
1. Introduction
According to WHO,unsafe abortion is one of the important reasons for maternal mortality and morbidity. Decriminalization of abortion is essential for promoting and protecting women’s health and life. However, the legalization of abortion services has remained a controversial issue in some countries. This research attempts to seek the answer for the following research question: What factors affect the legalization of abortion?) The influencing factors may include the degree of globalization, gender inequality level, economic development, the degree of education popularization. Two other special circumstances are also taken into consideration in this research, namely, whether abortion request is accepted as legal when pregnancy is the result of rape or incest, and whether threat to mother’s mental health is accepted as grounds for legal abortion. This report consists of five sections: In Section 1, the background and research question are presented; In Section 2, the data set used and variables included are described, and box plots and bar plots are used to visualize the distribution and relationships of variables; In Section 3, the methods employed in this research are introduced; In Section 4, the fit results of four models designed are presented, In section 5, the conclusions and the limitations of this report are discussed.
2. Data and Visualization
The dataset used is a Cross-Sectional dataset, named the Quality of Government (QoG) OECD (Cross-Sectional) CS Jan21 dataset. This dataset is collected by QoG Institute for academic-related purpose on quality of government study. It includes 1008 variables and 36 observations, and the data is from around 2017 with a range of +/- 3 years.
## ── Attaching packages ─────────────────────────────────────── tidyverse 1.3.1 ──
## ✓ ggplot2 3.3.3 ✓ purrr 0.3.4
## ✓ tibble 3.1.2 ✓ dplyr 1.0.6
## ✓ tidyr 1.1.3 ✓ stringr 1.4.0
## ✓ readr 1.4.0 ✓ forcats 0.5.1
## ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
## x dplyr::filter() masks stats::filter()
## x dplyr::lag() masks stats::lag()
## Loading required package: carData
##
## Attaching package: 'car'
## The following object is masked from 'package:dplyr':
##
## recode
## The following object is masked from 'package:purrr':
##
## some
## Registered S3 methods overwritten by 'lme4':
## method from
## cooks.distance.influence.merMod car
## influence.merMod car
## dfbeta.influence.merMod car
## dfbetas.influence.merMod car
## ResourceSelection 0.3-5 2019-07-22
## Loading required package: lattice
##
## Attaching package: 'caret'
## The following object is masked from 'package:purrr':
##
## lift
# load original data set
df <- read.csv(file = 'qog_oecd_cs_jan21.csv')
7 variables (i.e. cai_request, dr_ig, gii_gii, wdi_gdpcapcur, wef_lse, cai_rape, cai_mental) are selected from the original dataset based on the research question to form a filtered data and develop models.
df_filter <- df %>%
select(cai_request, gii_gii, wdi_gdpcapcur, wef_lse, dr_ig, cai_rape, cai_mental)
# make binary variables as factor
df_filter$cai_request <- as.factor(df_filter$cai_request)
df_filter$cai_rape <- as.factor(df_filter$cai_rape)
df_filter$cai_mental <- as.factor(df_filter$cai_mental)
summary(df_filter)
## cai_request gii_gii wdi_gdpcapcur wef_lse dr_ig
## 0:11 Min. :0.0410 Min. : 9288 Min. :14.23 Min. :71.49
## 1:25 1st Qu.:0.0655 1st Qu.: 20076 1st Qu.:16.15 1st Qu.:79.91
## Median :0.0990 Median : 39587 Median :16.52 Median :83.18
## Mean :0.1184 Mean : 39394 Mean :17.12 Mean :82.99
## 3rd Qu.:0.1313 3rd Qu.: 49954 3rd Qu.:18.24 3rd Qu.:87.43
## Max. :0.3360 Max. :107627 Max. :22.10 Max. :90.83
## cai_rape cai_mental
## 0: 3 0: 3
## 1:33 1:33
##
##
##
##
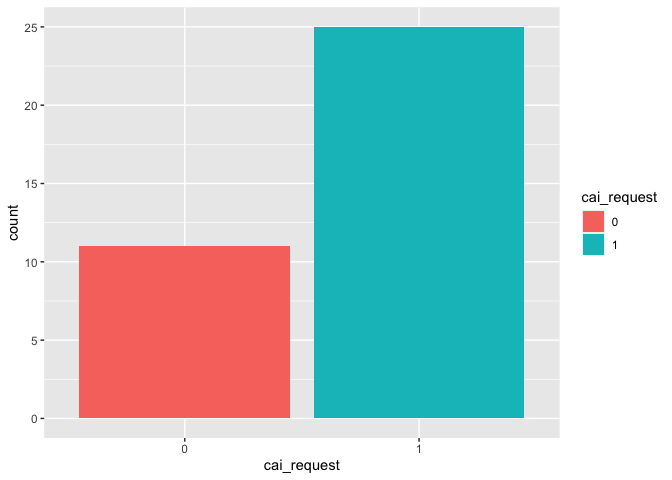
The response variable (cai_request) is a binary categorical variable, which codes whether abortion is available on request. 1 implies that there is complete access to abortion, and on the other hand, 0 indicates that abortion services are not legally available upon request.
# response cai_request
table(df_filter$cai_request)
##
## 0 1
## 11 25
# cai_request plot
g1 <- ggplot(df_filter, aes(x = cai_request, fill=cai_request)) +
geom_bar()
g1
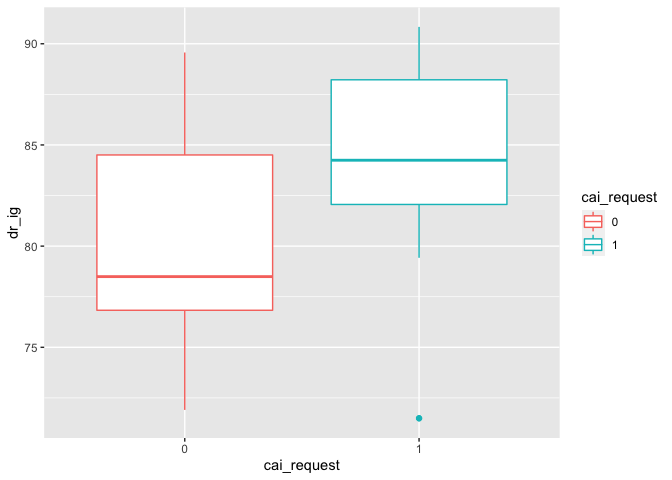
The explanatory variable (dr_ig) is a numeric variable, which is the overall weighted score of economic globalization, social globalization and political globalization. Bernal Santa-Olaya et al (1999) argue that the rise of women health movement benefit from and coincides with the development of global communications technology, economic globalization is leading the world into privatization and the reduction of public health services offered in the health care system, including reproductive health services. Therefore, it can be predict that the more globalized countries are, the more likely they are to accept the legalization of abortion.
# predictor dr_ig
g2 <- ggplot(df_filter, aes(x=cai_request, y=dr_ig, color=cai_request)) +
geom_boxplot()
g2
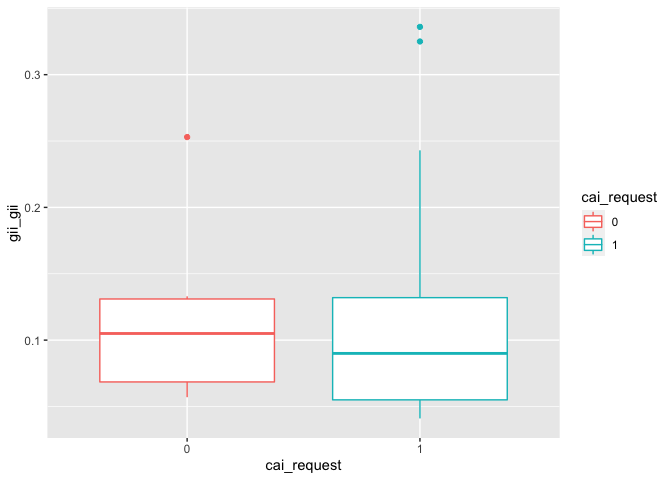
The dependent predictor (gii_gii) is also numeric variable, which describes gender inequality index. The higher the (gii_gii) value the more disparities between females and males and the more loss to human development.
# predictor gii_gii
g3 <- ggplot(df_filter, aes(x=cai_request, y=gii_gii, color=cai_request)) +
geom_boxplot()
g3
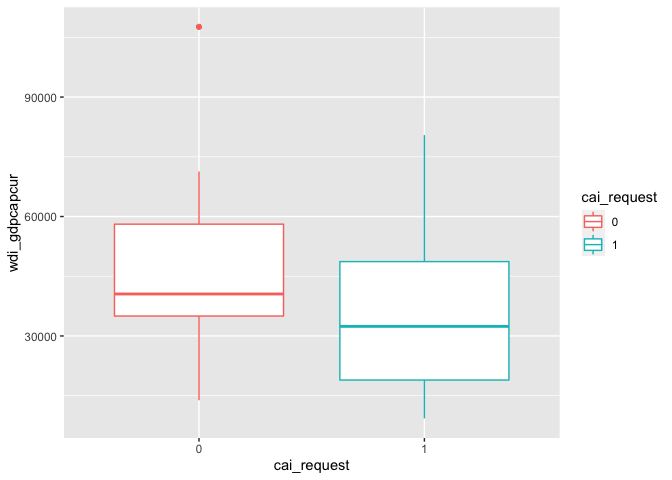
The numeric variable (wdi_gdpcapcur) is GDP per capita in current U.S. dollars, indicating gross domestic product divided by midyear population. Theoretically, the higher the GDP, the more prosperous the country’s economy.
# predictor wdi_gdpcapcur
g4 <- ggplot(df_filter, aes(x=cai_request, y=wdi_gdpcapcur, color=cai_request)) +
geom_boxplot()
g4
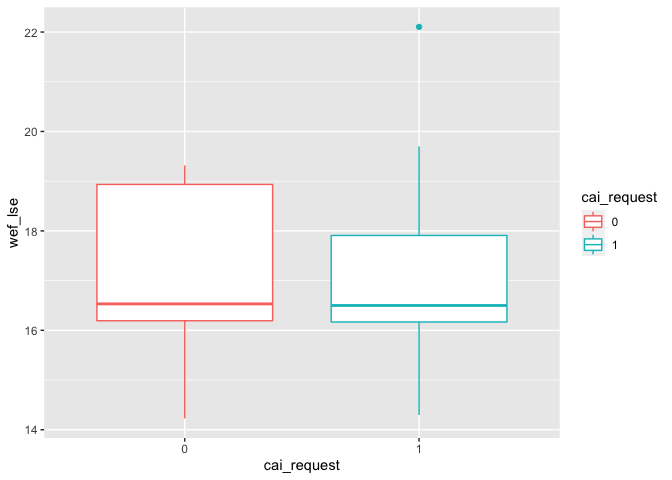
The numeric predictor “wef_lse” is the total number of years of schooling (primary through tertiary) that a child can expect to receive, which reflects education level of a country to some extent.
# predictor wef_lse
g5 <- ggplot(df_filter, aes(x=cai_request, y=wef_lse, color=cai_request)) +
geom_boxplot()
g5
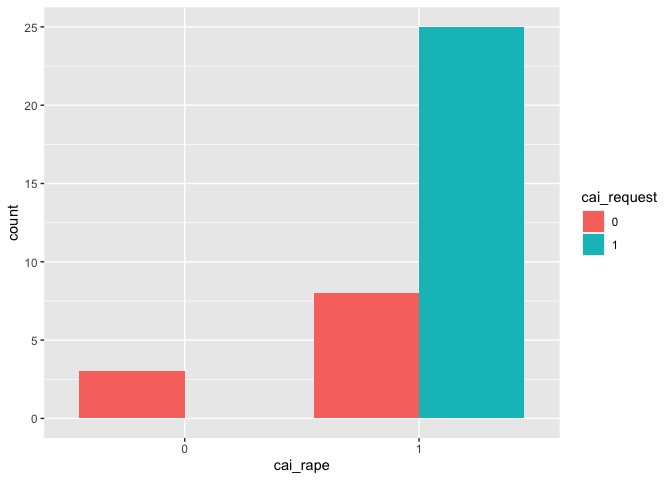
Besides, two special circumstances are also worth discussing. Thus two categorical variables, (cai_rape) and (cai_mental), are included as controlling variables, which indicate whether abortion request is accepted as legal when pregnancy is the result of rape or incest, and whether threat to mother’s mental health is accepted as grounds for legal abortion, respectively.
# controlling variable cai_rape
table(df_filter$cai_rape)
##
## 0 1
## 3 33
g6 <- ggplot(df_filter, aes(x = cai_rape, fill=cai_request)) +
geom_bar(position = position_dodge(preserve = "single"))
g6
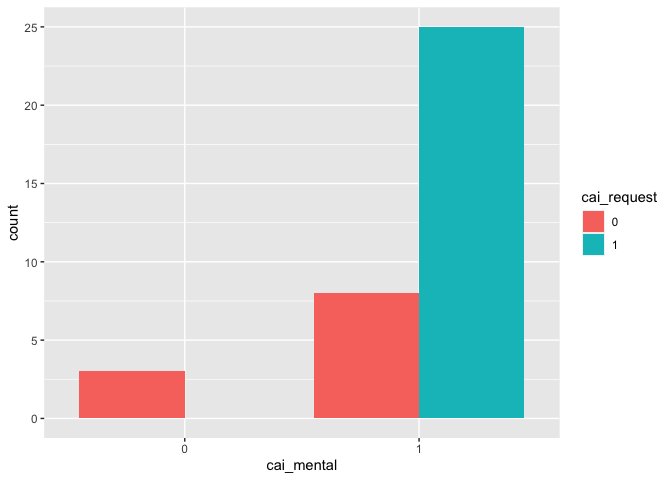
# controlling variable cai_mental
table(df_filter$cai_mental)
##
## 0 1
## 3 33
g7 <- ggplot(df_filter, aes(x = cai_mental, fill=cai_request)) +
geom_bar(position = position_dodge(preserve = "single"))
g7
3. Methods
Since the response variable, (cai_request), is a binary outcome, logistic regression model is designed to model differences in the likelihood of a binary outcome. Therefore, in this research, the logistic regression modelling was employed to predict whether the country approve the legalization of abortion.
In this research, 4 models are developed to explore the research question. The first model uses globalization index (dr_ig) as a main explanatory variable, controlling for (cai_rape) and (cai_mental). To test the effect of gender inequality, the second model adds (gii_gii) predictor based on the first model. In the third model, in order to test hypothesis that whether economy affect abortion legalization, thus this model concludes GDP per capita (wdi_gdpcapcur) as explanatory variable, controlling for the other variables listed above (including (dr_ig), and (gii_gii) ). On the basis of the above models, the last model considers the impact of education on the legalization of abortion, adding school life expectancy (wef_lse) as predictor.
4. Results
In this section, the fit results of the previously designed four models are presented, multicollinearity is checked, and binned residual plots are drawn to see how well the models fit.
4.1 Model results and Diagnostics
Model 1
Model 1 is designed to explore whether abortion legalization is affected by the globalization level. The main explanatory variable is (dr_ig), and with control for two special circumstances using variable (cai_rape) and variable (cai_mental) .
The summary of the Model 1 result is as follows:
# dr_ig + cai_rape + cai_mental
mod1 <- glm(cai_request ~ dr_ig + cai_rape + cai_mental,
data=df_filter,
family=binomial(link="logit"))
## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
summary(mod1)
##
## Call:
## glm(formula = cai_request ~ dr_ig + cai_rape + cai_mental, family = binomial(link = "logit"),
## data = df_filter)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.19229 -0.00005 0.43324 0.64614 1.41867
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -52.28874 6645.40235 -0.008 0.9937
## dr_ig 0.17623 0.08931 1.973 0.0485 *
## cai_rape1 20.54574 4699.00595 0.004 0.9965
## cai_mental1 18.59390 4699.00588 0.004 0.9968
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 44.316 on 35 degrees of freedom
## Residual deviance: 29.099 on 32 degrees of freedom
## AIC: 37.099
##
## Number of Fisher Scoring iterations: 18
According to the summary result, dr_ig is a significant predictor.
By computing variance inflation factor (VIF) and plotting the VIF plot, whether there is multicollinearity issue in Model 1 is checked.
t(t(vif(mod1)))
## [,1]
## dr_ig 1
## cai_rape 1
## cai_mental 1
plot(check_collinearity(mod1))
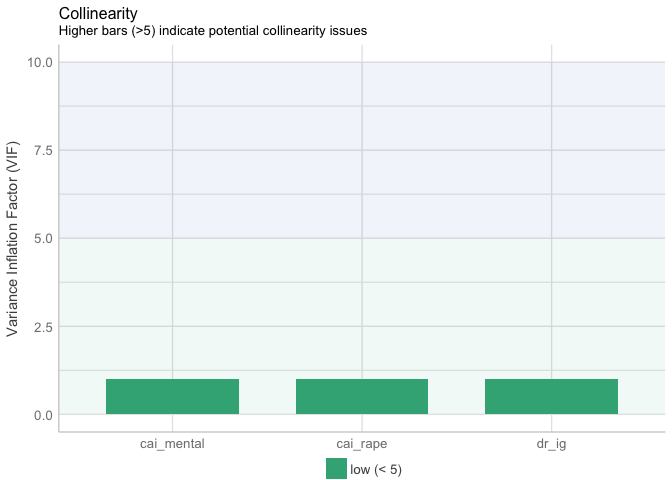
There is no multicollinearity issue found in Model 1.
Then, binned residual plot is drawn to check how many residual groups are outside the 95 percent confidence boundaries.
binned_residuals(mod1)
## Warning: Probably bad model fit. Only about 50% of the residuals are inside the error bounds.
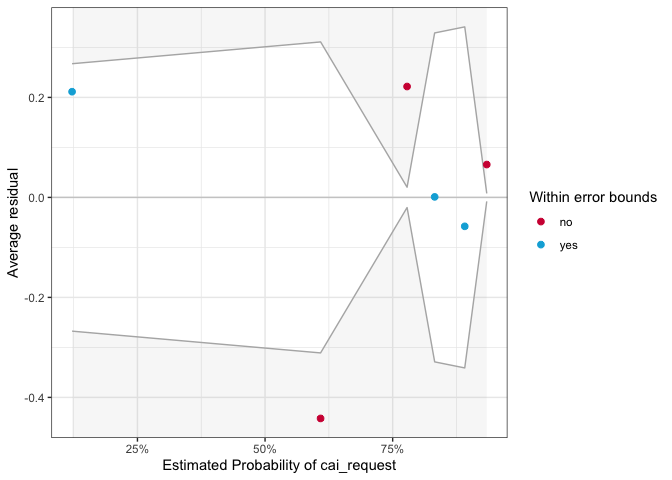
Model 1 probably has bad model fit, because only about 50% of the residuals are inside the error bounds.
Model 2
In model 2, the gender inequality index variable, (gii_gii) is added, and all the other variables in Model 1 are kept.
# gii_gii + dr_ig + cai_rape + cai_mental
mod2 <- glm(cai_request ~ gii_gii + dr_ig + cai_rape + cai_mental,
data=df_filter,
family=binomial(link="logit"))
## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
summary(mod2)
##
## Call:
## glm(formula = cai_request ~ gii_gii + dr_ig + cai_rape + cai_mental,
## family = binomial(link = "logit"), data = df_filter)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.32151 -0.00004 0.21198 0.46202 1.73407
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -88.7280 6834.4272 -0.013 0.9896
## gii_gii 33.8654 15.7072 2.156 0.0311 *
## dr_ig 0.5498 0.2184 2.518 0.0118 *
## cai_rape1 24.1181 4832.6489 0.005 0.9960
## cai_mental1 17.0805 4832.6485 0.004 0.9972
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 44.316 on 35 degrees of freedom
## Residual deviance: 18.859 on 31 degrees of freedom
## AIC: 28.859
##
## Number of Fisher Scoring iterations: 18
The summary result indicates that both (dr_ig) and (gii_gii) are significant predictors.
t(t(vif(mod2)))
## [,1]
## gii_gii 2.078325
## dr_ig 2.078325
## cai_rape 1.000000
## cai_mental 1.000000
plot(check_collinearity(mod2))
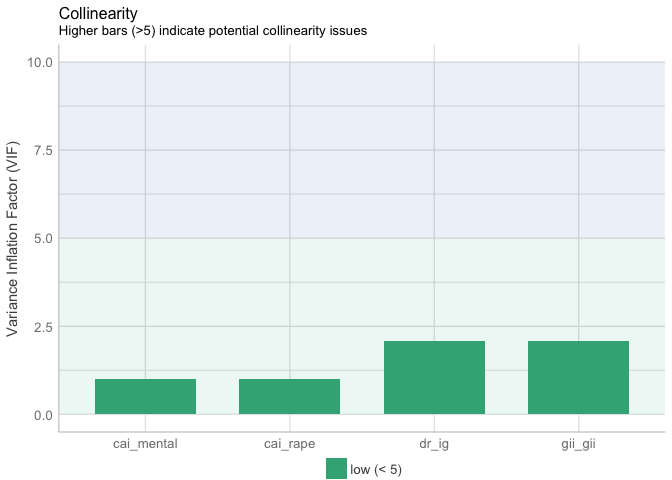
VIF of predictors in Model 2 are less than 5, therefore, there is no potential collinearity issues in Model 2.
binned_residuals(mod2)
## Warning: Probably bad model fit. Only about 67% of the residuals are inside the error bounds.
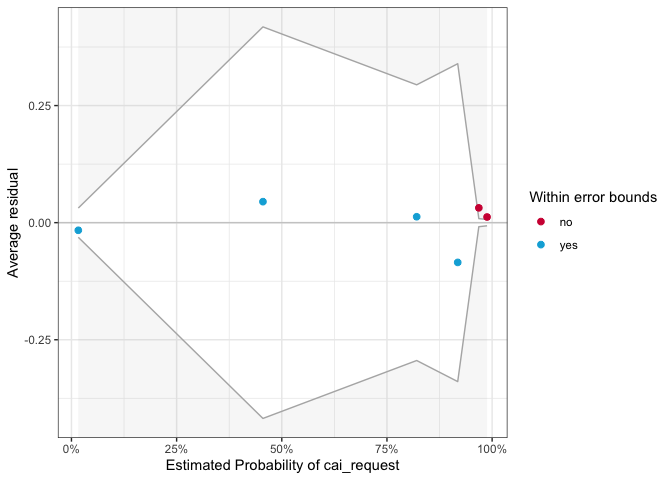
Only about 67% of the residuals are inside the error bounds. However, according to the residual figure, red dots occur at the ends of the distribution, and are not far from zero, thus there is no need to especially worry about this.
Model 3
In Model 3, variable (wdi_gdpcapcur), which give us information about the impact of country’s economy on abortion legalization, is added.
# wdi_gdpcapcur + gii_gii + dr_ig + cai_rape + cai_mental
mod3 <- glm(cai_request ~ wdi_gdpcapcur + gii_gii + dr_ig + cai_rape + cai_mental,
data=df_filter,
family=binomial(link="logit"))
## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
summary(mod3)
##
## Call:
## glm(formula = cai_request ~ wdi_gdpcapcur + gii_gii + dr_ig +
## cai_rape + cai_mental, family = binomial(link = "logit"),
## data = df_filter)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.42600 -0.00005 0.18135 0.37229 1.36592
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -8.894e+01 6.693e+03 -0.013 0.98940
## wdi_gdpcapcur -3.141e-05 2.839e-05 -1.106 0.26861
## gii_gii 2.849e+01 1.461e+01 1.951 0.05108 .
## dr_ig 5.747e-01 2.223e-01 2.585 0.00975 **
## cai_rape1 2.418e+01 4.733e+03 0.005 0.99592
## cai_mental1 1.708e+01 4.733e+03 0.004 0.99712
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 44.316 on 35 degrees of freedom
## Residual deviance: 17.451 on 30 degrees of freedom
## AIC: 29.451
##
## Number of Fisher Scoring iterations: 18
The summary result shows that variable (dr_ig) is still significant, however, variable (gii_gii) becomes moderately significant. Additionally, the new added variable (wdi_gdpcapcur) is not a significant predictor.
t(t(vif(mod3)))
## [,1]
## wdi_gdpcapcur 1.342772
## gii_gii 2.331198
## dr_ig 2.297954
## cai_rape 1.000000
## cai_mental 1.000000
plot(check_collinearity(mod3))
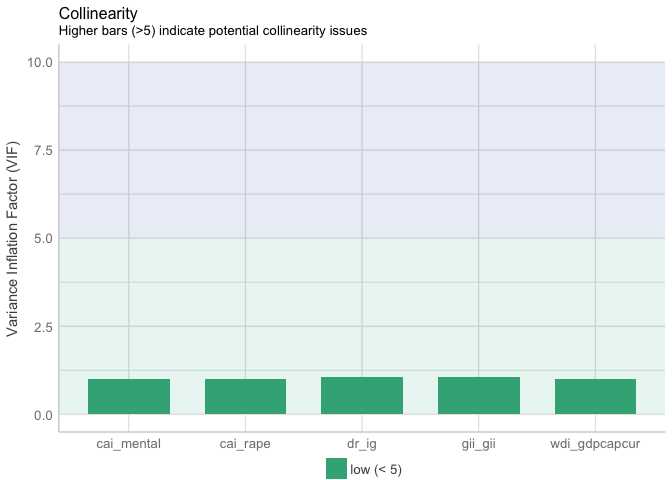
The VIF range between 1.00 and 2.33. It cannot be deduced that there does not exist multicollinearity issue in model 3.
binned_residuals(mod3)
## Warning: Probably bad model fit. Only about 67% of the residuals are inside the error bounds.
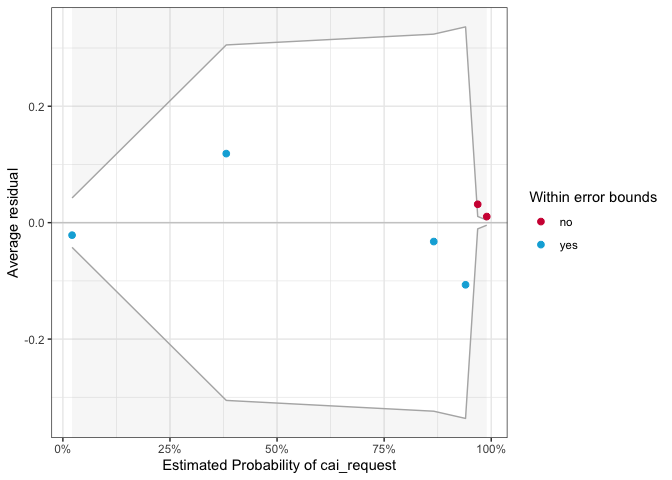
Only about 67% of the residuals are inside the error bounds. And the same as the residual plot of Model 2, red dots occur at the ends of the distribution, and are not far from zero, thus this is not a serious issue.
Model 4
Based on Model 3, variable (wef_lse) is added to find whether education level has an impact on whether abortion is available on request in model 4. Variable (wdi_gdpcapcur) is still included as predictor in Model 4 to maintain the theoretical completeness despite the fact that this variable is revealed to be not statistically significant.
# wef_lse + wdi_gdpcapcur + gii_gii + dr_ig + cai_rape + cai_mental
mod4 <- glm(cai_request ~ wef_lse + wdi_gdpcapcur + gii_gii + dr_ig + cai_rape + cai_mental,
data=df_filter,
family=binomial(link="logit"))
## Warning: glm.fit: fitted probabilities numerically 0 or 1 occurred
summary(mod4)
##
## Call:
## glm(formula = cai_request ~ wef_lse + wdi_gdpcapcur + gii_gii +
## dr_ig + cai_rape + cai_mental, family = binomial(link = "logit"),
## data = df_filter)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -2.48587 -0.00005 0.18436 0.39028 1.37195
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -9.047e+01 6.732e+03 -0.013 0.9893
## wef_lse 8.760e-02 3.308e-01 0.265 0.7911
## wdi_gdpcapcur -3.126e-05 2.939e-05 -1.064 0.2875
## gii_gii 2.881e+01 1.459e+01 1.975 0.0483 *
## dr_ig 5.744e-01 2.235e-01 2.570 0.0102 *
## cai_rape1 2.434e+01 4.760e+03 0.005 0.9959
## cai_mental1 1.690e+01 4.760e+03 0.004 0.9972
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 44.316 on 35 degrees of freedom
## Residual deviance: 17.379 on 29 degrees of freedom
## AIC: 31.379
##
## Number of Fisher Scoring iterations: 18
The newly added predictor (wef_lse) is not significant because the p-value is higher than 0.05. The predictors (dr_ig) and (gii_gii) are significant, and the significance of the variable (wdi_gdpcapcur) remains unchanged, not significant.
t(t(vif(mod4)))
## [,1]
## wef_lse 1.018550
## wdi_gdpcapcur 1.356143
## gii_gii 2.384422
## dr_ig 2.331092
## cai_rape 1.000000
## cai_mental 1.000000
plot(check_collinearity(mod4))
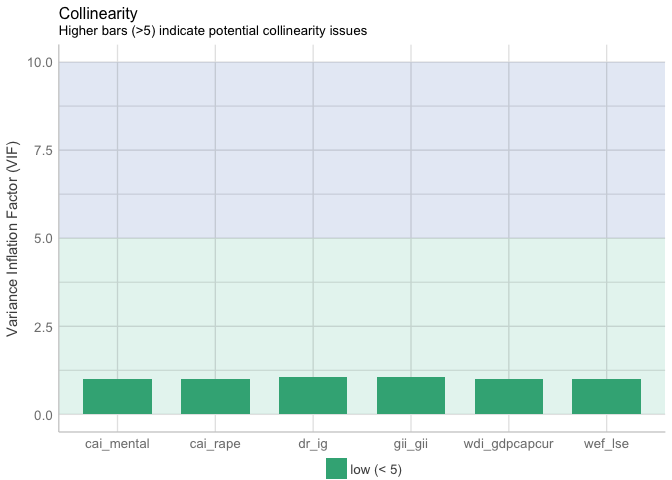
VIF of variables are low, therefore, it proves that there is no collinearity issues in Model 4.
binned_residuals(mod4)
## Warning: Probably bad model fit. Only about 67% of the residuals are inside the error bounds.
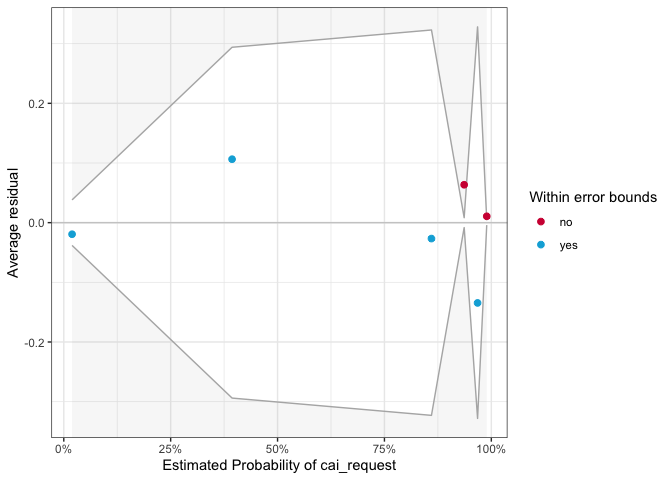
Only about 67% of the residuals are inside the error bounds. And the same as the residuals in Model 2 and Model 3, outliers in Model 4 are around zero, and occur at the ends of the distribution.
4.2 Model Selection
AIC value
By drawing the statistics table of four models, the best fit model can be selected based on the AIC values. To be specific, if there is a significant drop in AIC value, it is likely that model fit becomes better than previous one.
tab_model(mod4, mod3, mod2, mod1, show.ci = F, show.loglik = T, show.aic = T, show.r2 = F)
| cai\_request | cai\_request | cai\_request | cai\_request | |||||
|---|---|---|---|---|---|---|---|---|
| Predictors | Odds Ratios | p | Odds Ratios | p | Odds Ratios | p | Odds Ratios | p |
| (Intercept) | 0.00 | 0.989 | 0.00 | 0.989 | 0.00 | 0.990 | 0.00 | 0.994 |
| wef\_lse | 1.09 | 0.791 | ||||||
| wdi\_gdpcapcur | 1.00 | 0.287 | 1.00 | 0.269 | ||||
| gii\_gii | 3259656774933.23 | 0.048 | 2367175132884.29 | 0.051 | 509979183182613.69 | 0.031 | ||
| dr\_ig | 1.78 | 0.010 | 1.78 | 0.010 | 1.73 | 0.012 | 1.19 | 0.048 |
| cai\_rape \[1\] | 37211756733.55 | 0.996 | 31595758159.64 | 0.996 | 29808691658.80 | 0.996 | 837340769\.66 | 0.997 |
| cai\_mental \[1\] | 21851271.46 | 0.997 | 26053730.43 | 0.997 | 26178968.75 | 0.997 | 118912158\.12 | 0.997 |
| Observations | 36 | 36 | 36 | 36 | ||||
| AIC | 31.379 | 29.451 | 28.859 | 37.099 | ||||
| log-Likelihood | -8.689 | -8.726 | -9.430 | -14.550 | ||||
Model 2 has the lowest AIC value, 28.859. This indicates that Model 2 has better fit than other models.
AUC
ROC curve shows the trade-off between sensitivity and specificity. The area under the ROC Curve, which is also referred to as AUC, is a powerful metric to evaluate the performance of a binary classification model. The higher the value of AUC, the better the model performs.
test <- data.frame(resp = c(df_filter$cai_request),
mod1 = predict(mod1, df_filter, type="response"),
mod2 = predict(mod2, df_filter, type="response"),
mod3 = predict(mod3, df_filter, type="response"),
mod4 = predict(mod4, df_filter, type="response"))
test <- melt_roc(test, "resp", c("mod1", "mod2","mod3","mod4" ))
out <- ggplot(test, aes(d = D, m = M, colour = name)) +
geom_roc(n.cuts = 0) + style_roc(theme = theme_grey) + ggtitle("ROC Curves and AUC (Models 1-4)")
out + annotate("text", x = .75, y = .25, label = paste(paste(unique(test$name), "AUC =", round(calc_auc(out)$AUC, 2)), collapse = "\n"))
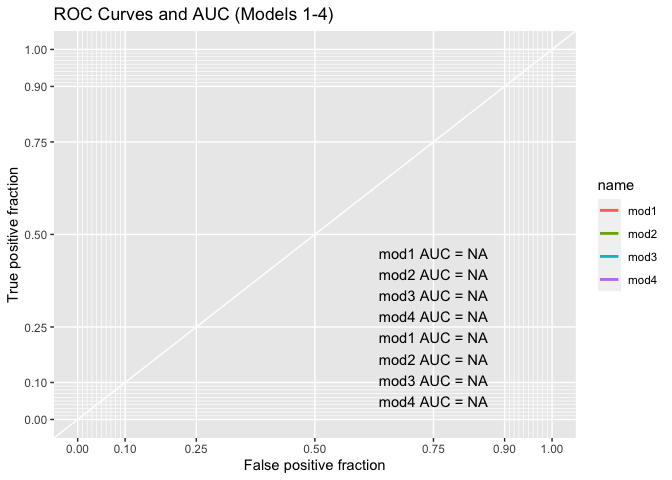
Model 2 and Model 3 has the highest AUC value, 0.94.
In terms of AIC and AUC performance, Model 2 is selected as the best model in this research.
4.3 The Interpretation of the Best Model
Goodness of fit
Firstly, the residual and null deviances can be used to test the following hypotheses: H0: All predictors are not related to the response variable. HA: At least one of the predictors are related to the response variable.
1 - pchisq(q=mod2$null.deviance - mod2$deviance, df=length(coef(mod2)))
## [1] 0.0001137127
According to the result, the p-value is nearly 0, therefore the null hypothesis is rejected, which means at least one of the predictors are related to the response variable.
Secondly, a table is drawn to look at the odds ratios of the best model, i.e. model 2. The coefficients with values above 1 increase the odds, while values below 1 decrease the odds of abortion legalization.
In the following table, the p-values of variables (dr_ig) and (gii_gii) are less than 0.05, which indicates they are significant predictors.
Variable (dr_ig) has an odds ratio of 1.73 and a p-value of 0.012, which means that the higher the degree of globalization, the more likely it is to legalize abortion request.
Variable (gii_gii) has an odds ratio of 509979183182613.69, and a p-value of 0.031, which indicates that the more disparities between females and males and the more likely the abortion request being considered legal.
As for the controlling variables(cai_rape) and (cai_mental), in special circumstances such as when pregnancy is the result of rape or incest or pregnancy is a threat to mother’s mental health, the odds of abortion request being accepted as legal also increase.
tab_model(mod2, show.ci = F, show.loglik = T, show.aic = T, show.r2 = F)
| cai\_request | ||
|---|---|---|
| Predictors | Odds Ratios | p |
| (Intercept) | 0.00 | 0.990 |
| gii\_gii | 509979183182613.69 | 0.031 |
| dr\_ig | 1.73 | 0.012 |
| cai\_rape \[1\] | 29808691658.80 | 0.996 |
| cai\_mental \[1\] | 26178968.75 | 0.997 |
| Observations | 36 | |
| AIC | 28.859 | |
| log-Likelihood | -9.430 | |
Confusion Matrix
Confusion matrix is an import measure that can be employed in binary classification scenario, which is consist of True Negative (TN), True Positive (TP), False, Positive (FP) and False Negative (FN).
A confusion matrix of Model 2 using threshold of 0.5 is drawn as follows:
draw_confusion_matrix <- function(cm) {
layout(matrix(c(1,1,2)))
par(mar=c(2,2,2,2))
plot(c(100, 345), c(300, 450), type = "n", xlab="", ylab="", xaxt='n', yaxt='n')
title('CONFUSION MATRIX', cex.main=2)
# create the matrix
rect(150, 430, 240, 370, col='#F7AD50')
text(195, 435, 'No', cex=1.2)
rect(250, 430, 340, 370, col='#3F97D0')
text(295, 435, 'Yes', cex=1.2)
text(125, 370, 'Predicted', cex=1.3, srt=90, font=2)
text(245, 450, 'Actual', cex=1.3, font=2)
rect(150, 305, 240, 365, col='#3F97D0')
rect(250, 305, 340, 365, col='#F7AD50')
text(140, 400, 'No', cex=1.2, srt=90)
text(140, 335, 'Yes', cex=1.2, srt=90)
# add in the cm results
res <- as.numeric(cm$table)
text(195, 400, res[1], cex=1.6, font=2, col='white')
text(195, 335, res[2], cex=1.6, font=2, col='white')
text(295, 400, res[3], cex=1.6, font=2, col='white')
text(295, 335, res[4], cex=1.6, font=2, col='white')
# add in the specifics
plot(c(100, 0), c(100, 0), type = "n", xlab="", ylab="", main = "DETAILS", xaxt='n', yaxt='n')
text(10, 50, names(cm$overall[1]), cex=1.2, font=2)
text(10, 30, round(as.numeric(cm$overall[1]), 3), cex=1.2)
text(30, 50, names(cm$byClass[2]), cex=1.2, font=2)
text(30, 30, round(as.numeric(cm$byClass[2]), 3), cex=1.2)
text(50, 50, names(cm$byClass[5]), cex=1.2, font=2)
text(50, 30, round(as.numeric(cm$byClass[5]), 3), cex=1.2)
text(70, 50, names(cm$byClass[6]), cex=1.2, font=2)
text(70, 30, round(as.numeric(cm$byClass[6]), 3), cex=1.2)
text(90, 50, names(cm$byClass[7]), cex=1.2, font=2)
text(90, 30, round(as.numeric(cm$byClass[7]), 3), cex=1.2)
}
# draw confusion matrix
probabilities <- predict(mod2, newdata = df_filter, type='response')
predicted.classes <- as.factor(ifelse(probabilities >= 0.5, "1", "0"))
# model accuracy
cfm1 <- confusionMatrix(predicted.classes, df_filter$cai_request, positive = '1')
draw_confusion_matrix(cfm1)
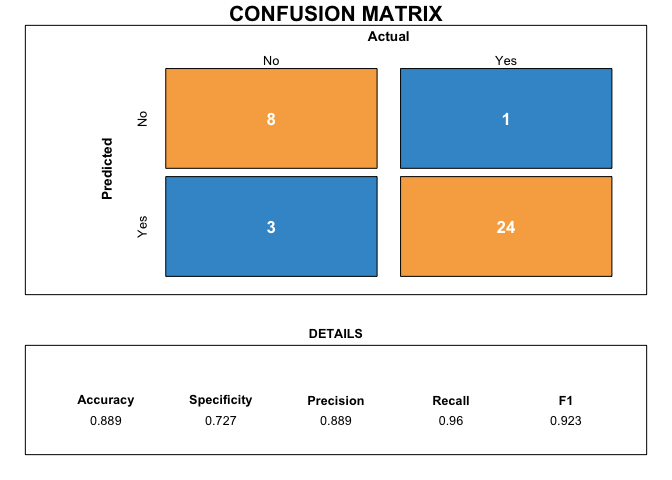
As shown in the confusion matrix, when setting threshold as 0.5, the accuracy of Model 2 is 0.889, the F1 score is 0.923, the recall is 0.96, and the specificity is 0.727.
ROC and AUC
The ROC curve of the best model is drawn in the following plot. The computed AUC is 0.94, which indicates the probability of 0.94 that a randomly chosen legal abortion allowed country is ranked higher than a randomly chosen legal abortion not allowed country by these models.
# draw ROC curve
test <- data.frame(resp = c(df_filter$cai_request),
mod2 = predict(mod2, df_filter, type="response"))
out <- ggplot(test, aes(d = resp, m = mod2)) +
geom_roc(n.cuts = 0) + style_roc(theme = theme_grey) + ggtitle("ROC Curves and AUC (Model 2)")
out + annotate("text", x = .75, y = .25, label = paste(paste(unique(test$name), "AUC =", round(calc_auc(out)$AUC, 2)), collapse = "\n"))
5. Conclusion
In order to seek the answer to the research question that what factors may affect the possibility of abortion being available on request, four models are developed in this research based on variables describing globalization level, gender inequality level, economics, and education level. Two special circumstances (rape, mother’s mental health) have also been taken into consideration. Since the response variable is a binary outcome, logistic regression model is used.
The best model is select based on AIC and AUC metrics. According to the final model results, the higher the degree of globalization, the more likely it is to legalize abortion request. The gender inequality index (gii_gii) is also proved as a significant predictor, however, it indicates that the more disparities between females and males and the more likely the abortion request being considered legal. This is a very weird finding, because according to common sense, if men and women are more unequal, women are less likely to obtain legal rights including abortion right. This may be due to the fact that I have overlooked some control variables, making the model biased. Additionally, sample size may also be the problem since there are only 36 observations in the dataset.
It is very interesting to find that economic level (wdi_gdpcapcur) and education level (wef_lse) are not significant predictors to predict whether the country approve the legalization of abortion. This may also due to the small data size, or it may be a problem of the variable selection.
From this analysis, we can infer that the more globalized countries are, the more likely they are to accept the legalization of abortion. Future research should try to use a time-series dataset with more observations instead of a sectional dataset with only 36 observations.
References:
[1] Bernal Santa-Olaya, E., Bissel, S. & Cortes, A. Effects of Globalization on the Efforts to Decriminalize Abortion in Mexico. Development 42, 130–133 (1999). https://doi.org/10.1057/palgrave.development.1110100
[2] Bozdogan, H. (1987). Model selection and Akaike’s Information Criterion (AIC): The general theory and its analytical extensions. Psychometrika, 52(3), 345–370. Retrieved from https://doi.org/10.1007/BF02294361
[3] Melo, F. (2013). Area under the ROC Curve. In W. Dubitzky, O. Wolkenhauer, K.-H. Cho, & H. Yokota (Eds.), Encyclopedia of Systems Biology (pp. 38–39). New York, NY: Springer New York. Retrieved from https://doi.org/10.1007/978-1-4419-9863-7_209